Miguel Angel te invitó a que pruebes Dropbox.

Hola: Miguel Angel desea que pruebes Dropbox. Dropbox te permite disponer de tus fotos, documentos y videos estés donde estés, además de compartirlos fácilmente. Aceptar invitación Gracias. - El equipo de Dropbox Si prefieres no recibir invitaciones de Dropbox, haz clic aquí. Dropbox, Inc., PO Box 77767, San Francisco, CA 94107 © 2014 Dropbox

Raíz cuadrada

En las ciencias matemáticas, se llama raíz cuadrada 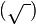de un número (a veces abreviada como raíz a secas) a aquel otro que siendo mayor o igual que cero, elevado al cuadrado, es igual al primero.

La raíz cuadrada de x se expresa:

Las raíces cuadradas fueron uno de los primeros desarrollos de las matemáticas, siendo particularmente investigadas durante el periodo pitagórico, cuando el descubrimiento de que laraíz cuadrada de 2 era irracional (inconmensurable) o no expresable como cociente alguno, lo que supuso un hito en la matemática de la época.

Posteriormente se fue ampliando la definición de raíz cuadrada. Para los números reales negativos, la generalización de la función raíz cuadrada de éstos da lugar al concepto de losnúmeros imaginarios y al cuerpo de los números complejos, algo necesario para que cualquier polinomio tenga todas sus raíces (teorema fundamental del álgebra). La diagonalizaciónde matrices también permite el cálculo rápido de la raíz de una matriz.

Ecuación de primer grado simple

Una ecuación es una igualdad que sólo se verifica para unos valores concretos de una variable, generalmente llamada x.

Resolver una ecuación consiste en hallar los valores de la variable que hacen cierta la igualdad.

Recuerda:

Si un elemento está sumando en un miembro pasa al otro restando. Si está restando pasa sumado.

Si un número multiplica a todos los elementos de un miembro pasa al otro dividiendo y si los divise pasa multiplicando.

A continuación les dejo un vídeo de como resolver ecuaciones de primer grado

GUIA PARA EXAMEN FLOR 1C

EL MAESTRO NOSDIO UNA GUIA O UNAS INSTRUCCIONES PARA ESTUDIAR Y ESTOS SON: ·PERIMETRO ·SUPERFISIE ·AREA ·SOLUCION DE PROBLEMAS DE PROPORCIONALIDAD(TIPO RESETA) ·EL AREA DEL CIRCULO ·DIVICION CON PUNTO DECIMAL ·SOLUCION DE ECUASIONES ·ECUACIONES ·CALCULO DE PERIMETRO PERO LOS TENIAMOS QUE ESTUDIAR Y ULTIMAMENTE Y ALGO DIFISILES JAJA BUENO ME DESPIDO .

LAS BALANZAS FLOR 1 - C

VIDEO BALANZA ASER LA VALANZA FUE LA INSPIRACION PARA RESOLVER LAS ECUASIONES O TAMBIEN LA PODEMOS DIBUJAR PERO TAMBIEN PUEDE SER DIBERTIDO YA QUE JUEGAS CON EL Y ADEMAS CONVIVES CONTUS COMPAÑEROS.

TECNICA.

LUNES 22 DE MARZO DEL 2011.

EL VIERNES 18 DE MARZO ISIMOS TECNICA BUENO COMO SIEMPRE LA ASEMOS TODOS LOS VIERNES

LA TECNICA TRATO DEECU LAS ASIONES:

1-50x+70=5593 YLA (X) SIGNIFICA=110.46

2-10X+34=74 YLA (X) SIGNIFICA=4

3-5X+15=3X+15 YLA (X) SIGNIFICA= 6 Y 10. EL RESULTADO = 45

4-12X+15018X+3 YLA (X) SIGNIFICA=2 Y 2. EL RESULTADO = 39

Y NOS DIO SU CORREO DE GMAIL QUE ES = elprofrmigeulengel@gmail.com

PASOS PARA UNA RAIZ CUADRADA.

Separa los dígitos de dos en dos. .
La mejor manera de explicar cómo se hace una raíz cuadrada es con un ejemplo. Vamos a hacer la raíz cuadrada del número 64.253. El número a partir de ahora se llamará radicando, el símbolo de la raíz será radical y cada cajetilla que abramos para hacer operaciones renglón de la raíz. El primer paso consiste en separar los dígitos del radicando de dos en dos de derecha a izquierda. Si hubiera decimales hay que dividir primero los enteros de derecha a izquierda y después la parte decimal a la inversa, de izquierda a derecha. En este caso no pueden quedar dígitos individuales, por lo que añadiremos un cero cuando lo necesitemos.

Busca un número que multiplicado por sí mismo se acerque a tu primer dígito. .
Hay que buscar un número cuyo cuadrado (multiplicar por si mismo) se acerque, nunca pase, la primera cifra del radicando, que en nuestro caso es 6. El número que encontremos lo apuntamos en el segundo renglón de la raíz, llamados auxiliares porque nos ayudan a descifrarla. La primera incógnita es 2, que al multiplicarse por si mismo da 4. Ese número hay que restarlo ahora al radicando (6-4) y anotar debajo el resultado (2).

Baja los otros dos dígitos y sigue la operación. .
Sigue estos pasos: Baja las dos siguientes cifras del radicando (42), sube la primera incógnita a la primera casilla (2) y escribe su doble en la tercera auxiliar. Una vez realizado esto seguimos con la operación. Vuelve a separar los dígitos del radicando que nos queda (242) dejando fuera la última cifra (2). Ahora divide el primer grupo de dígitos entre el número que haya en la tercera auxiliar (24/4). La cifra resultante la debes poner junto al dígito del tercer auxiliar y multiplicar por esa misma cifra (46X6) y comprobar que el resultado no es superior al radicando que tenemos. Si lo supera, debes bajar un número la incógnita.

Baja más dígitos y sube la segunda incógnita arriba. .
En nuestro ejemplo 46X6 son 276, lo que supera a 242, por lo que debemos utilizar el 5, y la operación es 45X5=225. Resta el resultado al radicando: 225-242=17. Ahora baja los siguientes dos dígitos (53) y después sube el 5 junto al 2.

En el cuarto renglón auxiliar escribe el doble de lo que tenga el primero. .
Llegados a este paso tenemos el radicando 1753 y en el cuarto auxiliar hay que poner el doble de los dos dígitos ya resueltos (25), que sería 50.

Separa el radicando y divide por la última incógnita. .
Volvemos a descartar el último número del radicando y nos queda 175. Lo volvemos a dividir por lo que ponga en el cuarto auxiliar, 175/50 y el resultado es 3 (hay que descartar los decimales). Volvemos a escribir la incógnita y multiplicar por ella misma: 503X3=1509.

Vuelve a restar. .
Restamos el resultado al radicando y nos queda 244.

Si no hay más dígitos se acaba la raíz cuadrada. .
La incógnita la volvemos a subir al renglón raíz y como ya no nos quedan más dígitos en el radicando, la raíz cuadrada se acaba. Si en el radicando hubiera decimales, deberiamos poner una coma junto al 253 y seguir resolviendo como los pasos anteriores.

Busca una calculadora... .
Si tienes cerca una calculadora te puedes ahorrar el resto de pasos. Si la calculadora que vas a utilizar es la del ordenador te enseñamos a hacerlo, porque no aparece el icono de raíz cuadrada. Lo primero es abrir la calculadora (Iniciio/Todos los programas/Accesorios/Calculadora). Después, despliega la pestaña 'Ver' y selecciona 'Científica'. A continuación, escribe el radicando, 64253, selecciona la palabra Inv. que está a la izquierda y pincha la tecla en rosa que encontrarás abajo donde indica x al cuadrado.
.

tecnica de 1 - c

VIERNES 25 DE FEBRERO DEL 2011.

E n el salón hicimos la técnica que el maestro MIGUEL ANGEL (de matemáticas) nos puso 6 preguntas y estas son las siguientes:

1_. Pepe a obtenido las siguientes calificaciones en los siguientes 5 periodos de matemáticas y desea saber cuál es su promedio:
8.7, 8.8, 9.1, 10 y 9.2.

R= 7.36

2_. Hugo, Paco y Luis reunieron 286 canicas y las van a repartir explica cual sería la mejor forma de hacerlo.

R= Mejor empiezo pro la división que se divide 285 entre 3 y nos da resultado de 95.33.Nos da a resultado si multiplicamos 95.33x3 nos da a resultado de 285, entonces nos sobra una canica pero a quien se las damos. Por eso lo mejor sería darle la canica a quien junto más canicas o echarla a un frasco y volver a comenzar
a juntar canicas.

3_. Para hacer un papalote chino se debe cubrir la superficie de un aro de bambú, si el radio es de este círculo es de 21.5 y consideramos Pi como 3.14. ¿Cuál SERIA EL AREA?

R= primero se multiplica 21.5 x 21.5=462.25 y luego multiplicas 462.25 x 3.14 = 1451.465 ese sería el resultado sería R=1451.465

4_. Para cubrir esa superficie circular de un papalote de 1451.465 cm 2
Hacerlo con 5 colores diferentes si se hace un reparto equitativo , ¿Qué cantidad de superficie cubrirá cada color?

R= Aquí primero se debe de dividir 1451.465 entre 5 para que nos dé la respuesta de 290.293 cm 2.

5_. En casa de Rafa se reunieron Lalo, Rosa y Arturo para hacer una tarea de español , como ya eran las 20hrs y aun no acababan se organizaron para pedir una pizza y refresco que dando en repartirse en partes iguales, ¿Cuánto debe aportar cada uno si el total fue de 212.55pesos?

R= Pues primero se divide para ver cuanto va a aportar cada quien para pagar lo mismo o la misma cantidad de dinero. Y entonces la división nos da el resultado de 53.175 como resultado Y ya lo multiplicas por 3 para que compruebes el resultado.

CUBOS MAGICOS

LUNES 21 DE FEBRERO DEL 2011.

HOY LUNES EN LO QUE EL MAESTRO LLEGABA NUESTRA MONITORA
ROSA (DE MATEMATICAS),NOS PUSO UNTRABAJO DE COMPLETAR UN
CUBO MAGICO.QUE DESIA ASI:

Completa el siguiente cuadro magico sumando sus lados
dando un resultado de = 15.siendo en todos los lados
con el resultado de quince(vertical ,horisontal y
diagonales).
Ese cubo seles mostrara al lado derecho.
15 15 15 15 15
15 4 9 2 15
15 3 5 7 15
15 8 1 6 15
15 15 15 15 15

graficas "1-c"

JUVES 10 DE FEBRERO DEL 2011.

HOY EL MAESTRO NOSDIO EL PROMEDIO DE LOS 3PERIODOS Y DIJO QUE MI FILA SACARA
EL PROMADIO DE EL 2PERIODO Y SALIMOS MUY BAJOS POR QUE EL RESULTADO FUE DE 7.7
PERO AQUI LO MALO ES QUE DE LAS CALIFICASIONES LA MAS AL TA FUE 6, DE HAY LE
SIGUE 8,DESPUES SIGUE 7 Y POR ULTIMO LAS CALIFICASIONES DE 10 Y DE 9 QUEDARON
EMPATES Y SON MUY POCAS PERSONAS LAS QUE SACARON 9 Y 10.

papalotes 1

MIERCOLES 9 DE FEBRERO DEL 2011.

HOY NOSOTROS NOSTOCO TRAER NUESTRO PAPALOTE Y EL MAESTRO SI NOLO REBISO PERO NOS DIJO QUE SALIERAMOS A LAS CANCHAS DE LA ESCUELA Y QUE SACARAMOS EL PAPALOTE PARA
BOLARLO PERO EL MIO NI QUISO BOLAR NADAMAS SE ALSO UN POCO, PERO SE QUISO QUEDAR EN EL PISO Y NO BOLAR.

papalotes

JUEVES 3 DE FEBRERO DEL 2011.

HOY TENEMOSQUE ASER UN PAPALOTE CON LA FORMA QUE NOSOTROS QUERAMOS HASTA LO
PODEMOS DISEÑARLO EN NUESTRO CUADERNO DE MATEMETICAS Y LLEBARLO A LA ESCUELA
PARA DE MOSTRAR QUE LO PODEMOS LLEBAR A LA ESCUELA TALBES EL LUNES 7 DE FEBRERO
DEL 2011.

Técnica

1° La señora rosa horneo 5.6 kg de galletas y debe hacer bolsitas de 250 gr ¿Cuántas bolsas llenara completamente?

4

250/1000 4 250

0 * 5 * 2

____ ______

20 500

llenara completamente 22 bolsas

2° El reloj de pared de mi mamá tiene un diámetro de 32cm si lo quiero rodear con un listón ¿Cuánto necesito? Considera pi=3.14

3.14 Necesitare 100.48 cm. de listón

* 32

________

628

942

_________

100.48

3° Si yo fui al Internet y me lleve $20 y la hora cuesta $10 y las impresiones $1.5 cada una , si tuve que sacar 3 impresiones y ocupe 1/2 hora el Internet ¿Cuánto fue y cuanto cambio me dieron?

5

2/10 1.50 4.50

0 * 3 + 5.00

______ _______

4.50 9.50

20.00

- 9.50

Gastara $9.50 y le sobrara $10.50

_____

10.50

Estas fueron algunas preguntas de la técnica y pues estas venian en el examen el cual el maestro nos dara la calificación mañana

matematicas de primero "c".

Miércoles 2 de febrero del 2011.
Hoy entregamos unos cubos de papiroflexia e isimos un examen que venía con varios problemas como el siguiente ejemplo:
1- La señora María horneo 5.6kg de galletas y debe hacer bolsitas de 325g ¿Cuántas bolsitas llenara completamente?
R= 22 Bolsitas.

Cómo subir trabajos al blog

Subir un vídeo y un trabajo en Internet es cosa fácil.

Y subir un vídeo es súper sencillo.

http://www.youtube.com/watch?v=RQMH6_VhQYI

operaciones con figuras de cubecrafft

problema datos operacion resultado

1º ¿Cuánto es si un lado de la cara mide 5x4x5 5x4= 20x5=100 100

2º¿Cuánto mide su cuerpo si sus medidas son 2.5x4x4 2.5x4=10x4=40 40

3º¿Cuánto miden cada uno de sus patas si miden 2x2.5x2x2 2x2.5=5x2=10x2=20 20

4º¿Cuánto miden cada uno de sus manos si miden 2x4x2x2 2x4=8x2=16x2=32 32

5º¿Cuánto mide su cuerpo con los resultados anteriores 100+40+20+32 100+40=140+20=160+32=192 192

OBJETIVO
Enseñar, y cultivar el aprendizaje de el juego de ajedrez por que sirve para agilizar tu mente y desarrollar tu cerebro mejor a parte te ayuda para competir con tus amigos.







¿QUE ES EL AJEDREZ?
El ajedrez es un deporte para dos jugadores, y uno de los juegos de mesa más populares del mundo. Se podría decir que es un juego de guerra, perteneciente a la misma familia que el xiàngqí (ajedrez chino) y el shōgi (ajedrez japonés). Se cree que todos ellos provienen del chaturanga, que se practicaba en la India en el siglo VI.
Ejemplo:






¿COMO ES EL AJEDREZ?
El ajedrez es una tabla de 64 cuadritos de la medida que tú quieras. El ajedrez 16 blancas y 16 negras y sus nombres son:
• TORRE
• CABALLO
• ALFIL
• REY
• REYNA
• ALFIL
• CABALLO
• TORRE

EL AJEDRES ANTES SE UTILISABA PARA LOS GERRAS Y LOS REYES LOS UTILISABAN PARA PLANEAR SUS ATAQUES DE GUERRA PARA SABER COMO MOVER SU EJERSITO.

Que son las matematicas

Las matemáticas siguieron desarrollándose, con continuas interrupciones, hasta que en el Renacimiento las innovaciones matemáticas interactuaron con los nuevos descubrimientos científicos. Como consecuencia, hubo una aceleración en la investigación que continúa hasta la actualidad.
Hoy en día, las Matemáticas se usan en todo el mundo como una herramienta esencial en muchos campos, entre los que se encuentran las ciencias naturales, la ingeniería, la medicina y las ciencias sociales, e incluso disciplinas que, aparentemente, no están vinculadas con ella, como la música (por ejemplo, en cuestiones de resonancia armónica). Las matemáticas aplicadas, rama de las matemáticas destinada a la aplicación de los conocimientos matemáticos a otros ámbitos, inspiran y hacen uso de los nuevos descubrimientos matemáticos y, en ocasiones, conducen al desarrollo de nuevas disciplinas. Los matemáticos también participan en las matemáticas puras, sin tener en cuenta la aplicación de esta ciencia, aunque las aplicaciones prácticas de las matemáticas puras suelen ser descubiertas con el paso del tiempo

Leyes de los signos

Leyes de los signos...

(suma resta

multiplicación división).

(suma resta)

signos iguales los números se suman y conservan el signos

signos diferentes los números se restan y conservan el signo del número mayor

signos iguales se multiplican o se dividen los números y el signo sera positivo

signos diferentes se multiplican o dividen y el signo y lo números serán negativos

AAAAA CHAVOS SE ME OLVIDO DECIRLES
QUE ESTUDIEN PARA EL EXAMEN ENTRANDO JAJA
ESTUDIAN EEEE QUE YO SI LO HARE COMO BUENA
ALUMNA AHY AJAAAA JAJA ESTUDIAN
AHORA SI

BYE

HOLA CHAVOS!!!!!!!!

PUES AQUI CONTANDOLES SOBRE MIS VACACIONES DIGO
NO VOY A SALIR BUUUU SOY POBRE..JAJA NO SE CREAN JAJA,
PUES LA VERDAD ESPERO QUE SE LA ESTEN PASANDO MUY LINDAS VACACIONES
Y PUES YO PUES AUNQUE NO HE SALIDO DE VACA ME LA HE PASADO BIEN
CON ANSIAS DE VER A MIS AMIGAS JAJA,Y PUES DE VERDAD LES DECEO UNAS
SUPER LINDAS VACACIONES SALE Y PUES A USTED MAESTRO SABE Q LO
ESTIMO MUCHO EEE, Y A TODOS LOS DEL SALON PUES OBVIO QUE TAMBIEN HAA,
Y ESPERO QUE LES HAYA GUSTADO EL NUEVO FONDO DEL BLOG...YO LO HICE
WIIIIIIIII...ESPERO QUE LES HAYA GUSTADO SALE ME VOY CHAVOS Y PROFE
ESPERO TEN BIEN Y SE LOS VUELVO A REPETIR LINDISIMAS VACACIONES SALE Y PUES
AQUI LES DEJO UNOS VIDEOS DE LAS CANCIONES QUE ME GUSTAN JEJE ESPERO LES GUSTE..

¡¡¡¡¡¡¡¡¡¡¡LOS ADORO!!!!!!!!!!!!!!!!



CUIDENSE MUCHO CHAVOS Y PROFE QUERIDISIMO!!!!!!

BESOS PA TODOS VALE...


BYE.

NUMEROS DECIMALES

NUMEROS DECIMALES

Los números fraccionarios decimales pueden expresarse en otra forma llamada número decimal. A su vez, los números decimales podrán también expresarse como fracciones. Las fracciones impropias están formadas por una parte entera y una parte fraccionaria. En cambio, las fracciones propias sólo tendrán parte fraccionaria ya que su parte entera es igual a cero

LINEAS ABIERTA Y CERRADAS

LINEAS ABIERTAS Y CERRADAS
Estas líneas sirven para formar figuras, cuando las líneas se combinan, y se unen el principio y el fin, se llaman líneas cerradas. Si se puede diferenciar en dos partes distintas, el principio y el fin de la línea, entonces son líneas abiertas.
Líneas cerradas
Líneas abiertas
Responde la siguiente pregunta: ¿Si cierras las líneas abiertas del dibujo anterior, qué obtienes? Mira dos ejemplos de objetos de la naturaleza, que puedas dibujar con líneas abiertas o líneas cerradas, por ejemplo, la luna, puedes dibujarla con una línea cerrada: Y las patas de un pollo, puedes dibujarlo usando líneas abiertas:
INTERIOR, EXTERIOR Y FRONTERA
Cuando tú tienes una línea cerrada, puedes observar otras cosas, que pueden estar dentro de esta línea cerrada, o en el interior, o fuera de la línea, o en el exterior. La línea cerrada, se llama frontera.

LIEN

FORMAS GEOMETRICAS Y FIGURAS PLANAS

Formas Geométricas y las figuras planas Existen muchas formas geométricas, aquí tenemos las más simples: El cuadrado, el triángulo y el rectángulo son figuras geométricas planas, formadas por líneas rectas cerradas. El círculo también es una figura plana pero a diferencia de las anteriores está formado por una línea curva cerrada. A estas figuras se les llaman planas porque parecieran que estuvieran acostadas sobre el papel. Vamos a ver cada una de estas figuras.
El cuadrado: Tiene cuatro lados iguales. Para dibujar el cuadrado siempre es bueno utilizar una regla milimetrada (con medidas), ya que los cuatro lados tienen que ser de igual longitud. Por consiguiente si sus cuatro lados son iguales sus cuatro ángulos deben ser del mismo tamaño, el cuadrado tiene los ángulos de 90°.
El ángulo se forma a partir de la unión de dos líneas. Al espacio comprendido entre esas dos líneas le llamamos ángulo y el punto de unión de las líneas le llamamos vértice.
	El triángulo: El triángulo, como lo dice la palabra "tri", está formado por tres lados y tres ángulos. A toda figura geométrica formada por tres lados sea grande, pequeña, alta, achatada... se le da el nombre de triángulo.
Clasificación de los triángulos según sus ángulos Entonces para dibujar un triángulo, necesitamos recordar que tiene tres lados, y tres ángulos que varían según el tamaño de las líneas y según el tipo de ángulos, y que todos los triángulos tienen tres vértices.
El rectángulo: Tiene cuatro lados, y si observas bien, iguales entre sí de dos en dos. Observa la imagen del rectángulo arriba, dos de sus lados son largos (estos están paralelos) comparados con los otros dos que son más cortos (también son paralelos).
Para dibujar el rectángulo siempre es bueno utilizar una regla, debido a las diferencias de longitud. Igualmente, los cuatro ángulos son de 90°. Para dibujar el rectángulo, necesitamos recordar que tiene dos lados iguales, largos y dos cortos también iguales entre sí, cuatro ángulos iguales, y cuatro vértices.
	EL círculo: El círculo tiene varios elementos que se deben tomar en cuenta, el centro, el radio, y la circunferencia de la línea que limita al círculo.
Para dibujar el círculo es necesario un compás, la apertura del compás dependerá de la longitud del radio, y éste a su vez determinará el tamaño del círculo. La punta del compás será el centro del círculo, y la mina del compás hará la circunferencia del círculo.
Para dibujar el círculo es necesario un compás, la apertura del compás dependerá de la longitud del radio, y éste a su vez determinará el tamaño del círculo. La punta del compás será el centro del círculo, y la mina del compás hará la circunferencia del círculo.
| Arriba | Volver a Primera Etapa Matemática | Página Principal |
Otros Temas: ¿Qué son los Números, cómo surgieron? Noción del número natural Suma Resta Valor de posición (unidad, decena, centena). La docena Divisibilidad Múltiplo Fracciones Relación entre Fracciones Unidades de medida Longitud Capacidad Tiempo Sistema monetario Números Romanos Noción de estadística Formas Geométricas Figuras Geométricas

EL CALENDARIO

"Dueño y señor" de años,
meses, semanas y días

¿Quién nos puede asegurar que acabamos de despedir el año 2006, y no el 2007 o el 2008?

Para llegar a algo tan sencillo como acercarse a un calendario para saber en qué día vivimos, científicos de todos los tiempos han tenido que corregir algunos errores y superar una que otra complicación.

El concepto del calendario se remonta a los pueblos primitivos, cuando su estructura se basaba únicamente en la salida y puesta del Sol, las fases de la Luna, las estaciones u otros ciclos de la naturaleza.

Pero la palabra "calendario" es posterior, de origen latino, y designaba el primer día de cada mes romano o Kalendas, formado por un conjunto de normas destinadas a la división del tiempo en períodos regulares y a poder fijar la fecha de ocurrencia de un hecho en relación con un origen determinado.

Actualmente, en la mayor parte de los países se usa el Calendario Solar. Se entiende por Calendario al conjunto de normas que permiten una máxima coincidencia del año civil con el año trópico. El año solar se toma por su relación con las estaciones del año.

El año solar o año trópico es el tiempo que toma la Tierra para hacer dos pasos sucesivos, por cualquiera de los equinoccios. Es tambien el tiempo de referencia del calendario actual y tiene un valor calculado de 365,2422 días.

De hecho, todas la dificultades del Calendario Solar radican en que la duración del año trópico no es un número exacto de días, sino que es igual a 365,24219879 días medios, con una disminución de aproximadamente medio segundo por siglo.

Los Mayas desarrollaron tres calendarios: - Uno de 365 días con 18 meses de 20 días, adicionando 5, los cuales eran considerados de mala suerte. - Un año sagrado de 260 días, inventado por los Zapotecas hacia el año 1000 a.C., que se usaba para planear la guerra, ofrecer sacrificios a los dioses y adivinar el futuro. Estaba relacionado con los ciclos de Venus. - Los dos anteriores se unían en otro, llamado el calendario "cerrado" o "redondo" que se cumplía con ciclos de 52 años. La terminación de este ciclo se esperaba con bastante temor pues podía suceder que el Sol no volviera a salir.

Como la medida del tiempo se basa en la repetición períodica de fenómenos astronómicos, los elementos fundamentales en los diferentes calendarios son el día, la semana, el mes y el año. De ellos, la semana es el más antiguo y el menos astronómico.

Según se tomen como elemento de referencia el Sol, la Luna o ambos, se tendrá el Calendario Solar, basado en la posición del Sol sobre el horizonte en su salida y puesta; Lunar, en relación a las fases de la Luna; y Lunisolar, que trata de combinar los dos anteriores.

Origen y evolución del calendario

En términos generales, el calendario solar dura 365 días, y el lunar 29.5.

Los babilonios iniciaron el uso del calendario lunar y descubrieron el ciclo metónico en el año 432 a.C, llamado así en honor al astrónomo griego Meton, quien descubrió que las fechas de las fases de la Luna se repetían exactamente luego de un período de 19 años.

En el norte de Europa, los celtas se regían por un calendario lunar, en el que la unidad de medida no era el día, sino la noche.

Por su parte, los egipcios optaron por el calendario de 365 días y un cuarto, cuyo inicio coincide con el 1 de enero.

De hecho, ellos son los precursores directos del calendario moderno que ahora usamos, pese a que en América, antes de la Conquista, los Mayas ya se regían por un calendario solar extraordinarimente exacto (ver recuadro).

Así las cosas, el calendario solar es el más difundido y el que más se usa actualmente.

Nuestro calendario actual fue adaptado en primera instancia por Julio César, a partir del Egipcio (este fue el calendario Juliano), quien eligió el inicio del año de una manera bastante arbitraria: modificó el calendario romano antiguo de 355 días que comprendía 10 meses, y decidió iniciar el año el 1 de marzo, aniversario de la fundación de Roma, en el 753 a.C.

Tenía 365 días, con algunos meses de 30 días y otros de 31, más un día suplementario cada cuatro años (el año bisiesto), en febrero, debido a que era el último mes del año romano.

EJERCICIOS RESUELTOS DE ALGEBRA

Comprobar que la relación definida en RxR de la forma (a,b)R(c,d) a² + b² = c² + d² es de equivalencia y representar gráficamente el conjunto cociente RxR/R.

Respuesta 2

Comprobamos que es relación de equivalencia :

Propiedad reflexiva :



Propiedad simétrica : Si (a,b)R(c,d) entonces (c,d)R(a,b) puesto que :



Propiedad transitiva : Si (a,b)R(c,d) y (c,d)R(e,f) entonces (a,b)R(e,f) puesto que :

La relación definida de ese modo en RxR es de equivalencia y el conjunto cociente RxR/R será el formado por las circunferencias del plano con centro en el origen.

EJERCICIOS RESUELTOS DE ALGEBRA

Estudiar si la relación definida en Z = {enteros} por aRb a + b múltiplo de 2, es de equivalencia y determinar el conjunto cociente en caso de que lo sea.

Respuesta 1

Para comprobar que la relación anterior es de equivalencia hacemos :

Propiedad reflexiva , ya que a+a = 2 a que es múltiplo de 2.

Propiedad simétrica : Si aRb entonces a+b es múltiplo de 2, pero a+b = b+a y, por lo tanto b+a es múltiplo de 2, esto es bRa.

Propiedad transitiva : Si aRb y bRc entonces a+b es múltiplo de 2 y b+c es múltiplo de 2. De ahí a+b+b+c = a + 2b + c es múltiplo de 2 y trivialmente a+c es múltiplo de 2 puesto que 2b siempre es múltiplo de 2. Por todo ello, aRc.

La relación así definida si es de equivalencia y el conjunto cociente es Z/R = {pares , impares}

ALGEBRA BASICA

Álgebra básica

Para trabajar en álgebra son necesarios ciertos conocimientos previos sobre operatoria en Números Enteros y Números Racionales. También deben conocerse las propiedades de las potencias.

Los ejercicios deben desarrollarse de acuerdo a las operatorias que se realicen. Se pueden restar o sumar términos semejantes, multiplicar expresiones algebraicas o bien simplificarlas.

Símbolos y términos específicos

Entre los símbolos algebraicos se encuentran números, letras y signos que representan las diversas operaciones aritméticas.

Los números son, por supuesto, constantes, pero las letras pueden representar tanto constantes como variables. Las primeras letras del alfabeto se usan para representar constantes y las últimas para variables.

Operaciones y agrupación de símbolos

La agrupación de los símbolos algebraicos y la secuencia de las operaciones aritméticas se basa en los símbolos de agrupación, que garantizan la claridad de lectura del lenguaje algebraico.

Entre los símbolos de agrupación se encuentran los paréntesis (), corchetes [], llaves {} y rayas horizontales —también llamadas vínculos— que suelen usarse para representar la división y las raíces, como en el siguiente ejemplo:

Los símbolos de las operaciones básicas son bien conocidos de la aritmética: adición (+), sustracción (-), multiplicación (×) y división (:).

En el caso de la multiplicación, el signo ‘×’ normalmente se omite o se sustituye por un punto, como en a·b. Un grupo de símbolos contiguos, como abc, representa el producto de a, b y c.

La división se indica normalmente mediante rayas horizontales. Una raya oblicua, o virgulilla, también se usa para separar el numerador, a la izquierda de la raya, del denominador, a la derecha, en las fracciones.

Hay que tener cuidado de agrupar los términos apropiadamente.

Por ejemplo, ax + b/c - dy indica que ax y dy son términos separados, lo mismo que b/c, mientras que (ax + b)/(c - dy) representa la fracción:

Prioridad de las operaciones

Primero se hacen las multiplicaciones, después las divisiones, seguidas de las sumas y las restas.

Los símbolos de agrupación indican el orden en que se han de realizar las operaciones: se hacen primero todas las operaciones dentro de un mismo grupo, comenzando por el más interno.

Por ejemplo:

Números Reales

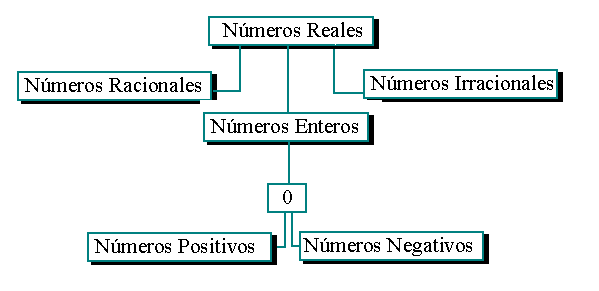
Los números que se utilizan en el álgebra son los números reales. Hay un número real en cada punto de la recta numérica.

Los números reales se dividen en números racionales, números irracionales y números enteros los cuales a su vez se dividen en números negativos, números positivos y cero (0).

Podemos verlo en esta tabla:

Técnica del 26 de febrero sobre ecuaciones

Has las siguientes ecuaciones

operacion resultado

1-. 6x-3=9 6x2=12-3=9 R=X=2

2-.3x-3.5=1 3x1.5=4.5-3.5=1 R=X=1.5

3-.6x+x-3=11 6x2=12+2=14-3=11 R=X=2

X/3-X/6+6=7 pasamos los tercios a sextos R=X=6

3/3=6/6=1+6=7

4-.5x-4=3.5 5x1.5=7.5-4=3.5 R=X=1.5

¿Qué es el álgebra? y su historia

El álgebra
El álgebra es la rama de las matemáticas que
estudia conceptos tales como vectores, matrices, sistemas de ecuaciones lineales y en un enfoque más formal, espacios vectoriales, y transformaciones lineales.
Es un área activa que tiene conexiones con muchas áreas dentro y fuera de las matemáticas como análisis funcional, ecuaciones diferenciales, investigación de operaciones, gráficas por computadora, ingeniería, etc.

La historia del álgebra
La historia del álgebra lineal moderna se remonta a los años de 1843 cuando William Rowan Hamilton (de quien proviene el uso del término vector) creó los cuaterniones; y de 1844 cuando Hermann Grassmann
publicó su libro Die lineale Ausdehnungslehre.

EDUARDO JAVIER

1.-Lineas rectas que al cortarse forman 4 ángulos iguales
R: PERPENDICULARES
2.-Porcion de plano limitada por una línea poligonal serrada es el tipo de figura queda determinada por sus lados que son los segmentos de la poligonal y por sus ángulos que son los que forman cada 2 lados
R: POLIGONO
3.-Que significa hacer una copia (1:2) del original
R: QUE CORRESPONDE A UN 20/1 DEL ORIGEN
4.-El área de u pentágono regular es 102.76cm cuadrados y su perímetro es de 38.64cm ¿Cuál es la longitud de su apotema?
R: 5.32
5.-Un engrane tiene 72 dientes y debe mover a uno de 21¿Cuáles el factor de proporcionalidad de dichos engranes?
R:24/7
6.-Un arbolito de navidad hechos de buenos deseos con una altura de 180 deberás dibujar l en la libreta de un escala 1:25 que altura debe tener el dibujo en libreta
R: 0.072
7.-Calcula el tamaño que tendrá un muñeco en su maqueta si esta elaborada con una escala de 1.200 y una persona promedio tiene una altura 1.70m
R: 0.0085
8.-Es la suma de todas sus longitudes de todos los lados de un polígono
R: PEIMETRO

sagacidad a prueba de la proporcionalidad

Sagacidad a Prueba

Lee cada uno de los siguientes problemas. Encuentra

la solución e indica si el problema es de prporcionalidad o no.

1. Agnese y Giulia corren a la misma velocidad en prueba alrededor de un circuito. Agnese comenzó primero y cuando llevaba recorridas 9 vueltas, Giulia había recorrido 3 vueltas. Cuando Giulia había recorrido 3 vueltas. Cuando Giulia completó 15 vueltas,

R= No es proporcional

2.El papá de Paolo compró 900 euros en $12 100.¿Cuánto tendría que pagar si comprara1 000 euros?

R= Sí es proporcional

3. La edad de Giovanni es 8 años más que la de Dino. Dino tiene

4 años más que Hugo, quien tiene 2 años.

R=No es proporcional

3.El costo de 6 refrescos es de $15. ¿Cuánto cuestan 9 refrescos?

R= Sí es proporcional

fELIz nAvIdad!!!!

HOLA CHICOS!!!
PZ PRIMERO Q NADA
LES QUIERO DESEAR UN
MUY PROSPERO AÑO
NUEVO Y Q DE TODO
CORAZON DIOS LOS
BENDIGA Y LLENE DE AMOR,
PAZ Y PROSPERIDAD ESTE
AÑO AAA Y A SACAR
BUENAS CALIFICACIONES
EEE CHICOS JEJE
Y DE VERDAD ESPERO
Y SE LA HAYAN
PASADO DE
MARAVILLA EN NAVIDAD
AAAA Y PUES YA LOS EXTRAÑO
AUNQ A MI AMIGA
DANIELA SE LA PASO
CONMIGO HACE RATITO
SE
LA PASO CONMIGO AKI
EN MI CASA LA DEJARON VENIR
WIIIII JEJE A ELLA
SI LA
VEO JEJE PERO
A USTEDES YA LOS EXTRAÑO JEJE
BUENO ESO ES TODO ESPERO
Q ESTE AÑO SE LLENE DE
AMOR.PAZ.PROSPERIDAD Y TODO
LES VAYA MEJOR LOS
QUIERO MUCHO
BUENO BYE


ATT:LAURA

Problemas del examen del de 17-11-09

1.-Rosario compro 3.5kg de manzanas a 24.90 el kilo ¿Cuánto pago por la manzanas?
R=87.15
2.-Un metro de tela cuesta 15.50 ¿Cuánto cuestan 8 metros de la misma tela?
R=23.5
3.-Cuantos ejes de simetría tiene un circulo
R=el numero seria infinito
4.-Cual es perímetro de un heptágono si mide por lado 3.5 cm
R=24.5cm
5.-Es el contorno de un figura y para calculo es la suma de todos los lados de la figura
R=perímetro

LA LINEA ROSA MIDE :7

LA LINEA VERDE MIDE:6

LA LINEA MORADA MIDE:3.5

LA LINEA NARANJA MIDE:3

Operaciones con fracciones
1.-6/15x12/16=2/1
2.-7/27x3/5=
3.-4/5 / 12/3=1/5
4.-15/24x4/12=5/24
5.-5/25 / 4/12=13/5
6.-8/60 / 1/8=1
7.-3/5-2/9=17/47
8.-15/40 / 2/10=7/40

figuras geometricas!!!

Figuras geométricas
Geometría. Polígonos: triángulo, cuadrado, rectángulo, rombo, trapecio, paralelogramo, pentágono, hexágono. Círculo. Área
Matemáticas /


Triangulo:

El triángulo es un polígono formado por tres lados y tres ángulos. La suma de todos sus ángulos siempre es 180 grados.

Para calcular el área se emplea la siguiente fórmula:

Área del triángulo = (base x altura) / 2

(tipos de triángulos: Isósceles, escaleno y equilátero)

Cuadrado:

El cuadrado es un polígono de cuatro lados, con la particularidad de que todos ellos son iguales. Además sus cuatro ángulos son de 90 grados cada uno.

El área de esta figura se calcula mediante la fórmula:

Área del cuadrado = lado al cuadrado

Rectángulo:


El rectángulo es un polígono de cuatro lados, iguales dos a dos. Sus cuatro ángulos son de 90 grados cada uno.

El área de esta figura se calcula mediante la fórmula:

Área del rectángulo = base.altura

Rombo:

El rombo es un polígono de cuatro lados iguales, pero sus cuatro ángulos son distintos de 90º.

El área de esta figura se calcula mediante la fórmula:

Área del rombo= (diagonal mayor x diagonal meno)/ 2

Trapecio:

El trapecio es un polígono de cuatro lados, pero sus cuatro ángulos son distintos de 90º.

El área de esta figura se calcula mediante la fórmula:

Área del trapecio = [(base mayor + base menor).altura] / 2

Paralelogramo:

El paralelogramo es un polígono de cuatro lados paralelos dos a dos.

El área de esta figura se calcula mediante la fórmula:

Área del paralelogramo = base.altura

Pentágono:

El pentágono regular es un polígono de cinco lados iguales y cinco ángulos iguales.

El área de esta figura se calcula mediante la fórmula:

Área del pentágono = (perímetro x apotema) / 2

Hexágono:

El hexágono regular es un polígono de seis lados iguales y seis ángulos iguales.

Los triángulos formados, al unir el centro con todos los vértices, son equiláteros.

El área de esta figura se calcula mediante la fórmula:

Área del hexágono = (perímetro x apotema) / 2

Circulo:

El círculo es la región delimitada por una circunferencia, siendo ésta el lugar geométrico de los puntos que equidistan del centro.

El área de esta figura se calcula mediante la fórmula:

Área del círculo = 3'14. radio al cuadrado

Una fracción propia es una fracción, distinta de cero, en la cual su numerador es menor que su denominador. En consecuencia, una fracción propia tiene un valor menor que la unidad.

Una fracción propia da cuenta de la idea de una porción o parte de un todo. Por ejemplo, en la expresión "tres cuartos superficie de la Tierra es agua", o "sólo la mitad de los asistentes pudo participar del concurso". De ahí se da la relación a un porcentaje.


El producto entre dos fracciones propias es siempre una fracción propia.

Ejemplos




Definiciones relacionadas. Una fracción impropia es una fracción que no es propia y que está escrita en la forma numerador/denominador.

Una fracción mixta es una forma especial de escritura de las fracciones impropias respecto de las fracciones propias. En efecto, como una fracción impropia s / d es igual a un número entero más una fracción propia, podemos escribir:



donde E y n son el cociente entero y el resto de la división entre s y d, y se cumple por tanto: s = Ed + n

Por ejemplo:

, y 16 = 3 * 5 + 1

Las expresiones con fracciones mixtas se observan usualmente en recetarios, donde puede leerse: "tres y media (31 / 2) cucharadas de ...".

Las fracciones propias con numerador 1 se denominan fracciones unitarias, y se designan por un medio, un tercio, etcétera.

LOS QUEBRADOS!!!

Números Fraccionarios
Propiedades Generales
Debido a mediciones u operaciones como la medición de las cantidades continuas o las divisiones inexactas, los números fraccionarios se han vuelto más importantes y necesarios en las matemáticas y la vida diaria.
NÚMERO FRACCIONARIO O QUEBRADO
Comúnmente conocido como fracción, el quebrado o número fraccionario es el que expresa 1 o más partes iguales de la unidad central. Según la cantidad en la que se divide la unidad, ésta va cambiando de nombre. Por ejemplo si está dividida en 2 se le llama medios, en 3 tercios, 4 cuartos, 5 quintos, 6 sextos, 7 séptimos, 8 octavos, 9 novenos, 10 décimos, etc…
Sus términos
La fracción está compuesta por 2 términos básicos, el numerador y el denominador.
El numerador menciona en cuantas partes se ha dividido la unidad, mientras el denominador indica cuantas partes se toman de la unidad.
Por ejemplo:
Su escritura
Una fracción tiene 2 formas de escribirse (notación). La primera es colocando una línea horizontal entre el numerador y el denominador. Por ejemplo:
La otra forma es colocando una línea diagonal entre ambos números. Por ejemplo:
9 / 5, 3 / 6, 10 / 8
Lectura
La forma para leer un quebrado es muy sencilla: primero se lee el numerador tal y como decimos comúnmente los números: un, dos, tres, cuatro, etc…
Con respecto al denominador lo leemos así: 2 es medios, 3 es tercios, 4 cuartos, 5 quintos, 6 sextos, 7 séptimos, 8 octavos, 9 novenos y 10 décimos.
En caso que el numerador sea mayor que 10, se le añade al número la terminación -avo. Con esa regla, podríamos decir que 11 se lee onceavo, 12 doceavo, 13 treceavo, etc...
Por ejemplo:
8 / 5 se lee ocho quintos
10 / 35 se lee diez treintaicincoavos
1
Clases
Podríamos decir que las fracciones se dividen en 2 tipos:
• Fracción Común: es la fracción cuyo denominador no es la unidad seguida de ceros. Por ejemplo:
8 / 3, 9 / 4
• Fracción Decimal: es la fracción que tiene como denominador la unidad seguida de ceros. Por ejemplo:
4 / 10, 48 / 100
Tipos
Toda fracción, sin importar que sea decimal o común, pueden ser fracciones:
• Propias: son las fracciones que tienen el numerador menor que el denominador. Por ejemplo:
9 / 13, 2 / 4, 5 / 12
• Impropias: son las fracciones que tienen el numerador mayor que el denominador. Por ejemplo:
15 / 4, 98 / 2, 8 / 7
• Unitarias: son las que tienen el mismo numerador y denominador. Por ejemplo:
4 / 4, 12 / 12, 9 / 9
• Número Mixto: una fracción mixta es aquella que contiene un número entero y una fracción. Por ejemplo:
1 3 / 4, 15 7 / 7
Algunas afirmaciones que podemos hacer con respecto a las fracciones son:
• Toda fracción propia es menor que la unidad.
• Toda fracción impropia es mayor que la unidad,
• Toda fracción unitaria es igual a la unidad
• Toda número mixto contiene un número exacto de unidades y además una o varias partes iguales a la unidad.
• De varias fracciones que tengan igual denominador es mayor la que tenga mayor denominador
• De varias fracciones que tengan el mismo numerador es mayor la que tenga menor denominador
• Si a los 2 términos de una fracción propia (numerador y denominador) se les suma un mismo número, la fracción nueva es mayor que la primera
2
• Si el numerador o el denominador de una fracción es multiplicado por cierto número, la nueva fracción queda multiplicada por dicho número y en caso que se divida, queda dividida.
• Si los 2 términos de una fracción se multiplican o dividen por un mismo número, la fracción no varía
• Si a los 2 términos de una fracción propia se le resta un mismo número, la nueva fracción es menor que la primera.
• Si a los 2 términos de una fracción impropia se les suma un mismo número, la fracción nueva es menor que la anterior, sin embargo si se les resta un mismo número la nueva fracción va a ser mayor que su antecesora.
Preguntas y respuestas de fracciones
¿Cómo convierto un número mixto en fracción impropia?
- Muy sencillo, se multiplica el entero por el denominador y el producto se le suma al numerador. El denominador es el mismo. Por ejemplo:
6 ½
En ese caso, se realiza la operación: 6 x 2 + 1. Así quedaría la fracción 13 / 2.
¿Cómo sé cuantos enteros hay en una fracción impropia?
• Se divide el numerador por el denominador. Si el cociente es exacto, el mismo representa los enteros, pero si la división es inexacta, el residuo es el numerador y el divisor es el denominador. Por ejemplo:
9 / 6 = 9:6 = 3 (número entero)
9 / 5 = 9: 5 = 4 (número entero)
¿Cómo reduzco un número entero a fracción?
• Existen 2 formas:
La más sencilla, que consiste en ponerle al número el denominador 1. Por ejemplo:
3 = 3 / 1, 24 = 24 / 1
Cuando se nos da un denominador específico, lo que se hace es multiplicar ese número por el denominador dado, de ese modo sacamos el numerador. El denominador es el que nos dieron. Por ejemplo:
Número entero = 13
Denominador dado = 5
13 x 5 = 65
Fracción = 65 / 5
3
¿Cómo puedo reducir o multiplicar una fracción?
• Para multiplicar una fracción lo único que se hace es multiplicar el numerador y denominador por el número dado o deseado. Por ejemplo:
3 / 9
3 x 3 = 9
9 x 3 = 27
Nueva fracción: 9 / 27
• Para reducir una fracción se divide el numerador y el denominador entre un número que pueda dividir a ambos de forma exacta. Por ejemplo:
24 / 12
24 : 2 = 12
12 : 2 = 6
Nueva fracción: 12 / 6
¿Qué es una fracción irreducible?
• Es la fracción que, como su nombre lo dice, no se puede reducir más utilizando factores primos. Esto ocurre porque el numerador y el de-
nominador son primos entre sí. Cuando una fracción es irreducible se dice que esta en su más simple expresión o a su mínima expresión. Por ejemplo:
7 / 5, 20 / 33
Si nosotros eleváramos una fracción irreducible a una potencia, la fracción que resulta es también irreducible
¿A qué se refiere el término “simplificación de fracciones”?
• Esta expresión se refiere a convertir una fracción en otra equivalente cuyos términos (denominador y numerador) sean menores. Para eso se dividen sus 2 términos sucesivamente por los factores comunes que tengan. Por ejemplo:
500 / 125 : 5 = 100 / 25 : 5 = 25 / 5 : 5 / 1

El diagrama del árbol

Un diagrama del árbol es un arreglo en el que en una primera columnase pone un conjunto de opciones; luego por cada opción en la primera columna se abre una 2da columna con otro conjunto de opciones, unidas mediante segmentos (ramas).
El siguiente ejemplo aclara cómo construir un diagrama de árbol.

En una asamblea se quiere elegir, de entre 4candidatos (Jared, Auliya, Sherezada y Omar) un comité de 2 personas: una como presidente y otra como secretario.Cada uno puede ser presidente o secretario, pero no ocupar los 2 cargos a la vez. ¿Cuántos comités diferentes podríamos formar?

Presidente Secretario

Omar (Jared,Omar)
Jared Sherezada (Jared,Sherezada)
Auliya (Jared,Auliya)

Jared (Omar,Jared)
Omar Sherezada (Omar,Sherezada)
Auliya (Omar,Auliya)

Jared (Sherezada,Jared)
Sherezada Omar (Sherezada,Omar)
Auliya (Sherezada,Auliya)

Jared (Auliya,Jared)
Auliya Omar (Auliya,Omar)
Sherezada (Auliya,Sherezada)

Entonces, es posible formar 12 comités diferentes.

Técnica

6/10 x 12/6
3/5 x 6/3=18/15=6/5

7/21 x 3/5
1/3 x 3/5=3/15=1/5

4/5 / 12/3
4/5 / 4/1=1/5

15/24 x 4/12
5/8 x 1/3=5/24

5/25 / 4/12
1/5 / 1/3=3/5

8/64 / 1/8
1/8 / 1/8=8/8=4/4=2/2=1/1

3/5 - 2/9=17/45

15/40 - 2/10
5/8 - 1/5= 7/40

caminos diferentes

c a m i n o s ... d i f e r e n t e s

Esta actividad está dirigida a estudiantes de primero de secundaria en adelante.
Se trata de resolver problemas de álgebra que fueron inventados por un matemático francés del siglo XV: Nicolás Chuquet.
Si sabes álgebra puedes intentar resolverlos usándola, si no usa tu intuición y tu sentido común pues al fin en matemáticas se puede llegar a una solución por caminos muy distintos.


Problema 1
Un hombre gasta 1/3 de su dinero y pierde 2/3 de lo que le quedó. Le quedan al final 12 monedas. ¿Cuántas monedas tenía al pri R=54 monedas tenia al principio

Problema 2
Una pieza de tela se tiñe de la siguiente manera: 1/3 y 1/4 de ella de color negro y los 8 metros sobrantes de gris. ¿Cuántos metros tenía la pieza?
R=19.2 metros de

Problema 3
Un mercader visita tres ferias; en la primera duplica su dinero y gasta treinta monedas de oro, en la segunda triplica su dinero y gasta 54 monedas de oro, en la tercera cuadruplica su dinero y gasta 72 monedas de oro. Al final le quedan 48 monedas de oro. ¿Con cuántas monedas empezó su recorrido por las ferias?
R=con 29 monedas empezó su recorrido por las ferias

Problema 4
Un carpintero accede a trabajar con las siguientes condiciones: recibirá 5.50 por cada día que asista a trabajar y él pagará 6.60 cada día que falte a trabajar. Al final de 30 días terminó "tablas", es decir, recibió tanto dinero como el que pagó. ¿Cuántos días asistió a trabajar y cuántos faltó?
R=16 dias asistio y 14 dias faltó

Problema 5
Para lograr que su hijo se interesara en el estudio de la aritmética el padre le ofrece lo siguiente: le pagará 8 céntimos por cada problema que resuelva bien y le cobrará 5 céntimos por cada uno que esté mal resuelto. Al final de 26 problemas ninguno de los dos le debe dinero al otro. ¿Cuántos problemas resolvió correctamente el hijo?
R= resolvió 10 problemas correctamente


Problema 6
Un sirviente va a recibir 100 monedas de oro y una capa por un año de trabajo. Después de 7 meses decide dejar el empleo y recibe la capa y 20 monedas de oro. ¿Cuánto valía la capa?
R=80 monedas de oro