Cómo subir trabajos al blog

Subir un vídeo y un trabajo en Internet es cosa fácil.

Y subir un vídeo es súper sencillo.

http://www.youtube.com/watch?v=RQMH6_VhQYI

operaciones con figuras de cubecrafft

problema datos operacion resultado

1º ¿Cuánto es si un lado de la cara mide 5x4x5 5x4= 20x5=100 100

2º¿Cuánto mide su cuerpo si sus medidas son 2.5x4x4 2.5x4=10x4=40 40

3º¿Cuánto miden cada uno de sus patas si miden 2x2.5x2x2 2x2.5=5x2=10x2=20 20

4º¿Cuánto miden cada uno de sus manos si miden 2x4x2x2 2x4=8x2=16x2=32 32

5º¿Cuánto mide su cuerpo con los resultados anteriores 100+40+20+32 100+40=140+20=160+32=192 192

OBJETIVO
Enseñar, y cultivar el aprendizaje de el juego de ajedrez por que sirve para agilizar tu mente y desarrollar tu cerebro mejor a parte te ayuda para competir con tus amigos.







¿QUE ES EL AJEDREZ?
El ajedrez es un deporte para dos jugadores, y uno de los juegos de mesa más populares del mundo. Se podría decir que es un juego de guerra, perteneciente a la misma familia que el xiàngqí (ajedrez chino) y el shōgi (ajedrez japonés). Se cree que todos ellos provienen del chaturanga, que se practicaba en la India en el siglo VI.
Ejemplo:






¿COMO ES EL AJEDREZ?
El ajedrez es una tabla de 64 cuadritos de la medida que tú quieras. El ajedrez 16 blancas y 16 negras y sus nombres son:
• TORRE
• CABALLO
• ALFIL
• REY
• REYNA
• ALFIL
• CABALLO
• TORRE

EL AJEDRES ANTES SE UTILISABA PARA LOS GERRAS Y LOS REYES LOS UTILISABAN PARA PLANEAR SUS ATAQUES DE GUERRA PARA SABER COMO MOVER SU EJERSITO.

Que son las matematicas

Las matemáticas siguieron desarrollándose, con continuas interrupciones, hasta que en el Renacimiento las innovaciones matemáticas interactuaron con los nuevos descubrimientos científicos. Como consecuencia, hubo una aceleración en la investigación que continúa hasta la actualidad.
Hoy en día, las Matemáticas se usan en todo el mundo como una herramienta esencial en muchos campos, entre los que se encuentran las ciencias naturales, la ingeniería, la medicina y las ciencias sociales, e incluso disciplinas que, aparentemente, no están vinculadas con ella, como la música (por ejemplo, en cuestiones de resonancia armónica). Las matemáticas aplicadas, rama de las matemáticas destinada a la aplicación de los conocimientos matemáticos a otros ámbitos, inspiran y hacen uso de los nuevos descubrimientos matemáticos y, en ocasiones, conducen al desarrollo de nuevas disciplinas. Los matemáticos también participan en las matemáticas puras, sin tener en cuenta la aplicación de esta ciencia, aunque las aplicaciones prácticas de las matemáticas puras suelen ser descubiertas con el paso del tiempo

Leyes de los signos

Leyes de los signos...

(suma resta

multiplicación división).

(suma resta)

signos iguales los números se suman y conservan el signos

signos diferentes los números se restan y conservan el signo del número mayor

signos iguales se multiplican o se dividen los números y el signo sera positivo

signos diferentes se multiplican o dividen y el signo y lo números serán negativos

AAAAA CHAVOS SE ME OLVIDO DECIRLES
QUE ESTUDIEN PARA EL EXAMEN ENTRANDO JAJA
ESTUDIAN EEEE QUE YO SI LO HARE COMO BUENA
ALUMNA AHY AJAAAA JAJA ESTUDIAN
AHORA SI

BYE

HOLA CHAVOS!!!!!!!!

PUES AQUI CONTANDOLES SOBRE MIS VACACIONES DIGO
NO VOY A SALIR BUUUU SOY POBRE..JAJA NO SE CREAN JAJA,
PUES LA VERDAD ESPERO QUE SE LA ESTEN PASANDO MUY LINDAS VACACIONES
Y PUES YO PUES AUNQUE NO HE SALIDO DE VACA ME LA HE PASADO BIEN
CON ANSIAS DE VER A MIS AMIGAS JAJA,Y PUES DE VERDAD LES DECEO UNAS
SUPER LINDAS VACACIONES SALE Y PUES A USTED MAESTRO SABE Q LO
ESTIMO MUCHO EEE, Y A TODOS LOS DEL SALON PUES OBVIO QUE TAMBIEN HAA,
Y ESPERO QUE LES HAYA GUSTADO EL NUEVO FONDO DEL BLOG...YO LO HICE
WIIIIIIIII...ESPERO QUE LES HAYA GUSTADO SALE ME VOY CHAVOS Y PROFE
ESPERO TEN BIEN Y SE LOS VUELVO A REPETIR LINDISIMAS VACACIONES SALE Y PUES
AQUI LES DEJO UNOS VIDEOS DE LAS CANCIONES QUE ME GUSTAN JEJE ESPERO LES GUSTE..

¡¡¡¡¡¡¡¡¡¡¡LOS ADORO!!!!!!!!!!!!!!!!



CUIDENSE MUCHO CHAVOS Y PROFE QUERIDISIMO!!!!!!

BESOS PA TODOS VALE...


BYE.

NUMEROS DECIMALES

NUMEROS DECIMALES

Los números fraccionarios decimales pueden expresarse en otra forma llamada número decimal. A su vez, los números decimales podrán también expresarse como fracciones. Las fracciones impropias están formadas por una parte entera y una parte fraccionaria. En cambio, las fracciones propias sólo tendrán parte fraccionaria ya que su parte entera es igual a cero

LINEAS ABIERTA Y CERRADAS

LINEAS ABIERTAS Y CERRADAS
Estas líneas sirven para formar figuras, cuando las líneas se combinan, y se unen el principio y el fin, se llaman líneas cerradas. Si se puede diferenciar en dos partes distintas, el principio y el fin de la línea, entonces son líneas abiertas.
Líneas cerradas
Líneas abiertas
Responde la siguiente pregunta: ¿Si cierras las líneas abiertas del dibujo anterior, qué obtienes? Mira dos ejemplos de objetos de la naturaleza, que puedas dibujar con líneas abiertas o líneas cerradas, por ejemplo, la luna, puedes dibujarla con una línea cerrada: Y las patas de un pollo, puedes dibujarlo usando líneas abiertas:
INTERIOR, EXTERIOR Y FRONTERA
Cuando tú tienes una línea cerrada, puedes observar otras cosas, que pueden estar dentro de esta línea cerrada, o en el interior, o fuera de la línea, o en el exterior. La línea cerrada, se llama frontera.

LIEN

FORMAS GEOMETRICAS Y FIGURAS PLANAS

Formas Geométricas y las figuras planas Existen muchas formas geométricas, aquí tenemos las más simples: El cuadrado, el triángulo y el rectángulo son figuras geométricas planas, formadas por líneas rectas cerradas. El círculo también es una figura plana pero a diferencia de las anteriores está formado por una línea curva cerrada. A estas figuras se les llaman planas porque parecieran que estuvieran acostadas sobre el papel. Vamos a ver cada una de estas figuras.
El cuadrado: Tiene cuatro lados iguales. Para dibujar el cuadrado siempre es bueno utilizar una regla milimetrada (con medidas), ya que los cuatro lados tienen que ser de igual longitud. Por consiguiente si sus cuatro lados son iguales sus cuatro ángulos deben ser del mismo tamaño, el cuadrado tiene los ángulos de 90°.
El ángulo se forma a partir de la unión de dos líneas. Al espacio comprendido entre esas dos líneas le llamamos ángulo y el punto de unión de las líneas le llamamos vértice.
	El triángulo: El triángulo, como lo dice la palabra "tri", está formado por tres lados y tres ángulos. A toda figura geométrica formada por tres lados sea grande, pequeña, alta, achatada... se le da el nombre de triángulo.
Clasificación de los triángulos según sus ángulos Entonces para dibujar un triángulo, necesitamos recordar que tiene tres lados, y tres ángulos que varían según el tamaño de las líneas y según el tipo de ángulos, y que todos los triángulos tienen tres vértices.
El rectángulo: Tiene cuatro lados, y si observas bien, iguales entre sí de dos en dos. Observa la imagen del rectángulo arriba, dos de sus lados son largos (estos están paralelos) comparados con los otros dos que son más cortos (también son paralelos).
Para dibujar el rectángulo siempre es bueno utilizar una regla, debido a las diferencias de longitud. Igualmente, los cuatro ángulos son de 90°. Para dibujar el rectángulo, necesitamos recordar que tiene dos lados iguales, largos y dos cortos también iguales entre sí, cuatro ángulos iguales, y cuatro vértices.
	EL círculo: El círculo tiene varios elementos que se deben tomar en cuenta, el centro, el radio, y la circunferencia de la línea que limita al círculo.
Para dibujar el círculo es necesario un compás, la apertura del compás dependerá de la longitud del radio, y éste a su vez determinará el tamaño del círculo. La punta del compás será el centro del círculo, y la mina del compás hará la circunferencia del círculo.
Para dibujar el círculo es necesario un compás, la apertura del compás dependerá de la longitud del radio, y éste a su vez determinará el tamaño del círculo. La punta del compás será el centro del círculo, y la mina del compás hará la circunferencia del círculo.
| Arriba | Volver a Primera Etapa Matemática | Página Principal |
Otros Temas: ¿Qué son los Números, cómo surgieron? Noción del número natural Suma Resta Valor de posición (unidad, decena, centena). La docena Divisibilidad Múltiplo Fracciones Relación entre Fracciones Unidades de medida Longitud Capacidad Tiempo Sistema monetario Números Romanos Noción de estadística Formas Geométricas Figuras Geométricas

EL CALENDARIO

"Dueño y señor" de años,
meses, semanas y días

¿Quién nos puede asegurar que acabamos de despedir el año 2006, y no el 2007 o el 2008?

Para llegar a algo tan sencillo como acercarse a un calendario para saber en qué día vivimos, científicos de todos los tiempos han tenido que corregir algunos errores y superar una que otra complicación.

El concepto del calendario se remonta a los pueblos primitivos, cuando su estructura se basaba únicamente en la salida y puesta del Sol, las fases de la Luna, las estaciones u otros ciclos de la naturaleza.

Pero la palabra "calendario" es posterior, de origen latino, y designaba el primer día de cada mes romano o Kalendas, formado por un conjunto de normas destinadas a la división del tiempo en períodos regulares y a poder fijar la fecha de ocurrencia de un hecho en relación con un origen determinado.

Actualmente, en la mayor parte de los países se usa el Calendario Solar. Se entiende por Calendario al conjunto de normas que permiten una máxima coincidencia del año civil con el año trópico. El año solar se toma por su relación con las estaciones del año.

El año solar o año trópico es el tiempo que toma la Tierra para hacer dos pasos sucesivos, por cualquiera de los equinoccios. Es tambien el tiempo de referencia del calendario actual y tiene un valor calculado de 365,2422 días.

De hecho, todas la dificultades del Calendario Solar radican en que la duración del año trópico no es un número exacto de días, sino que es igual a 365,24219879 días medios, con una disminución de aproximadamente medio segundo por siglo.

Los Mayas desarrollaron tres calendarios: - Uno de 365 días con 18 meses de 20 días, adicionando 5, los cuales eran considerados de mala suerte. - Un año sagrado de 260 días, inventado por los Zapotecas hacia el año 1000 a.C., que se usaba para planear la guerra, ofrecer sacrificios a los dioses y adivinar el futuro. Estaba relacionado con los ciclos de Venus. - Los dos anteriores se unían en otro, llamado el calendario "cerrado" o "redondo" que se cumplía con ciclos de 52 años. La terminación de este ciclo se esperaba con bastante temor pues podía suceder que el Sol no volviera a salir.

Como la medida del tiempo se basa en la repetición períodica de fenómenos astronómicos, los elementos fundamentales en los diferentes calendarios son el día, la semana, el mes y el año. De ellos, la semana es el más antiguo y el menos astronómico.

Según se tomen como elemento de referencia el Sol, la Luna o ambos, se tendrá el Calendario Solar, basado en la posición del Sol sobre el horizonte en su salida y puesta; Lunar, en relación a las fases de la Luna; y Lunisolar, que trata de combinar los dos anteriores.

Origen y evolución del calendario

En términos generales, el calendario solar dura 365 días, y el lunar 29.5.

Los babilonios iniciaron el uso del calendario lunar y descubrieron el ciclo metónico en el año 432 a.C, llamado así en honor al astrónomo griego Meton, quien descubrió que las fechas de las fases de la Luna se repetían exactamente luego de un período de 19 años.

En el norte de Europa, los celtas se regían por un calendario lunar, en el que la unidad de medida no era el día, sino la noche.

Por su parte, los egipcios optaron por el calendario de 365 días y un cuarto, cuyo inicio coincide con el 1 de enero.

De hecho, ellos son los precursores directos del calendario moderno que ahora usamos, pese a que en América, antes de la Conquista, los Mayas ya se regían por un calendario solar extraordinarimente exacto (ver recuadro).

Así las cosas, el calendario solar es el más difundido y el que más se usa actualmente.

Nuestro calendario actual fue adaptado en primera instancia por Julio César, a partir del Egipcio (este fue el calendario Juliano), quien eligió el inicio del año de una manera bastante arbitraria: modificó el calendario romano antiguo de 355 días que comprendía 10 meses, y decidió iniciar el año el 1 de marzo, aniversario de la fundación de Roma, en el 753 a.C.

Tenía 365 días, con algunos meses de 30 días y otros de 31, más un día suplementario cada cuatro años (el año bisiesto), en febrero, debido a que era el último mes del año romano.

EJERCICIOS RESUELTOS DE ALGEBRA

Comprobar que la relación definida en RxR de la forma (a,b)R(c,d) a² + b² = c² + d² es de equivalencia y representar gráficamente el conjunto cociente RxR/R.

Respuesta 2

Comprobamos que es relación de equivalencia :

Propiedad reflexiva :



Propiedad simétrica : Si (a,b)R(c,d) entonces (c,d)R(a,b) puesto que :



Propiedad transitiva : Si (a,b)R(c,d) y (c,d)R(e,f) entonces (a,b)R(e,f) puesto que :

La relación definida de ese modo en RxR es de equivalencia y el conjunto cociente RxR/R será el formado por las circunferencias del plano con centro en el origen.

EJERCICIOS RESUELTOS DE ALGEBRA

Estudiar si la relación definida en Z = {enteros} por aRb a + b múltiplo de 2, es de equivalencia y determinar el conjunto cociente en caso de que lo sea.

Respuesta 1

Para comprobar que la relación anterior es de equivalencia hacemos :

Propiedad reflexiva , ya que a+a = 2 a que es múltiplo de 2.

Propiedad simétrica : Si aRb entonces a+b es múltiplo de 2, pero a+b = b+a y, por lo tanto b+a es múltiplo de 2, esto es bRa.

Propiedad transitiva : Si aRb y bRc entonces a+b es múltiplo de 2 y b+c es múltiplo de 2. De ahí a+b+b+c = a + 2b + c es múltiplo de 2 y trivialmente a+c es múltiplo de 2 puesto que 2b siempre es múltiplo de 2. Por todo ello, aRc.

La relación así definida si es de equivalencia y el conjunto cociente es Z/R = {pares , impares}

ALGEBRA BASICA

Álgebra básica

Para trabajar en álgebra son necesarios ciertos conocimientos previos sobre operatoria en Números Enteros y Números Racionales. También deben conocerse las propiedades de las potencias.

Los ejercicios deben desarrollarse de acuerdo a las operatorias que se realicen. Se pueden restar o sumar términos semejantes, multiplicar expresiones algebraicas o bien simplificarlas.

Símbolos y términos específicos

Entre los símbolos algebraicos se encuentran números, letras y signos que representan las diversas operaciones aritméticas.

Los números son, por supuesto, constantes, pero las letras pueden representar tanto constantes como variables. Las primeras letras del alfabeto se usan para representar constantes y las últimas para variables.

Operaciones y agrupación de símbolos

La agrupación de los símbolos algebraicos y la secuencia de las operaciones aritméticas se basa en los símbolos de agrupación, que garantizan la claridad de lectura del lenguaje algebraico.

Entre los símbolos de agrupación se encuentran los paréntesis (), corchetes [], llaves {} y rayas horizontales —también llamadas vínculos— que suelen usarse para representar la división y las raíces, como en el siguiente ejemplo:

Los símbolos de las operaciones básicas son bien conocidos de la aritmética: adición (+), sustracción (-), multiplicación (×) y división (:).

En el caso de la multiplicación, el signo ‘×’ normalmente se omite o se sustituye por un punto, como en a·b. Un grupo de símbolos contiguos, como abc, representa el producto de a, b y c.

La división se indica normalmente mediante rayas horizontales. Una raya oblicua, o virgulilla, también se usa para separar el numerador, a la izquierda de la raya, del denominador, a la derecha, en las fracciones.

Hay que tener cuidado de agrupar los términos apropiadamente.

Por ejemplo, ax + b/c - dy indica que ax y dy son términos separados, lo mismo que b/c, mientras que (ax + b)/(c - dy) representa la fracción:

Prioridad de las operaciones

Primero se hacen las multiplicaciones, después las divisiones, seguidas de las sumas y las restas.

Los símbolos de agrupación indican el orden en que se han de realizar las operaciones: se hacen primero todas las operaciones dentro de un mismo grupo, comenzando por el más interno.

Por ejemplo:

Números Reales

Los números que se utilizan en el álgebra son los números reales. Hay un número real en cada punto de la recta numérica.

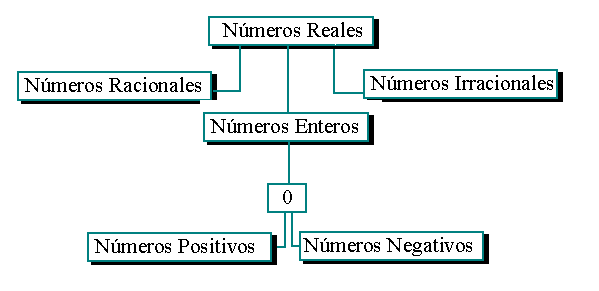
Los números reales se dividen en números racionales, números irracionales y números enteros los cuales a su vez se dividen en números negativos, números positivos y cero (0).

Podemos verlo en esta tabla:

Técnica del 26 de febrero sobre ecuaciones

Has las siguientes ecuaciones

operacion resultado

1-. 6x-3=9 6x2=12-3=9 R=X=2

2-.3x-3.5=1 3x1.5=4.5-3.5=1 R=X=1.5

3-.6x+x-3=11 6x2=12+2=14-3=11 R=X=2

X/3-X/6+6=7 pasamos los tercios a sextos R=X=6

3/3=6/6=1+6=7

4-.5x-4=3.5 5x1.5=7.5-4=3.5 R=X=1.5

¿Qué es el álgebra? y su historia

El álgebra
El álgebra es la rama de las matemáticas que
estudia conceptos tales como vectores, matrices, sistemas de ecuaciones lineales y en un enfoque más formal, espacios vectoriales, y transformaciones lineales.
Es un área activa que tiene conexiones con muchas áreas dentro y fuera de las matemáticas como análisis funcional, ecuaciones diferenciales, investigación de operaciones, gráficas por computadora, ingeniería, etc.

La historia del álgebra
La historia del álgebra lineal moderna se remonta a los años de 1843 cuando William Rowan Hamilton (de quien proviene el uso del término vector) creó los cuaterniones; y de 1844 cuando Hermann Grassmann
publicó su libro Die lineale Ausdehnungslehre.

EDUARDO JAVIER

1.-Lineas rectas que al cortarse forman 4 ángulos iguales
R: PERPENDICULARES
2.-Porcion de plano limitada por una línea poligonal serrada es el tipo de figura queda determinada por sus lados que son los segmentos de la poligonal y por sus ángulos que son los que forman cada 2 lados
R: POLIGONO
3.-Que significa hacer una copia (1:2) del original
R: QUE CORRESPONDE A UN 20/1 DEL ORIGEN
4.-El área de u pentágono regular es 102.76cm cuadrados y su perímetro es de 38.64cm ¿Cuál es la longitud de su apotema?
R: 5.32
5.-Un engrane tiene 72 dientes y debe mover a uno de 21¿Cuáles el factor de proporcionalidad de dichos engranes?
R:24/7
6.-Un arbolito de navidad hechos de buenos deseos con una altura de 180 deberás dibujar l en la libreta de un escala 1:25 que altura debe tener el dibujo en libreta
R: 0.072
7.-Calcula el tamaño que tendrá un muñeco en su maqueta si esta elaborada con una escala de 1.200 y una persona promedio tiene una altura 1.70m
R: 0.0085
8.-Es la suma de todas sus longitudes de todos los lados de un polígono
R: PEIMETRO

sagacidad a prueba de la proporcionalidad

Sagacidad a Prueba

Lee cada uno de los siguientes problemas. Encuentra

la solución e indica si el problema es de prporcionalidad o no.

1. Agnese y Giulia corren a la misma velocidad en prueba alrededor de un circuito. Agnese comenzó primero y cuando llevaba recorridas 9 vueltas, Giulia había recorrido 3 vueltas. Cuando Giulia había recorrido 3 vueltas. Cuando Giulia completó 15 vueltas,

R= No es proporcional

2.El papá de Paolo compró 900 euros en $12 100.¿Cuánto tendría que pagar si comprara1 000 euros?

R= Sí es proporcional

3. La edad de Giovanni es 8 años más que la de Dino. Dino tiene

4 años más que Hugo, quien tiene 2 años.

R=No es proporcional

3.El costo de 6 refrescos es de $15. ¿Cuánto cuestan 9 refrescos?

R= Sí es proporcional

fELIz nAvIdad!!!!

HOLA CHICOS!!!
PZ PRIMERO Q NADA
LES QUIERO DESEAR UN
MUY PROSPERO AÑO
NUEVO Y Q DE TODO
CORAZON DIOS LOS
BENDIGA Y LLENE DE AMOR,
PAZ Y PROSPERIDAD ESTE
AÑO AAA Y A SACAR
BUENAS CALIFICACIONES
EEE CHICOS JEJE
Y DE VERDAD ESPERO
Y SE LA HAYAN
PASADO DE
MARAVILLA EN NAVIDAD
AAAA Y PUES YA LOS EXTRAÑO
AUNQ A MI AMIGA
DANIELA SE LA PASO
CONMIGO HACE RATITO
SE
LA PASO CONMIGO AKI
EN MI CASA LA DEJARON VENIR
WIIIII JEJE A ELLA
SI LA
VEO JEJE PERO
A USTEDES YA LOS EXTRAÑO JEJE
BUENO ESO ES TODO ESPERO
Q ESTE AÑO SE LLENE DE
AMOR.PAZ.PROSPERIDAD Y TODO
LES VAYA MEJOR LOS
QUIERO MUCHO
BUENO BYE


ATT:LAURA