Raíz cuadrada

En las ciencias matemáticas, se llama raíz cuadrada 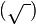de un número (a veces abreviada como raíz a secas) a aquel otro que siendo mayor o igual que cero, elevado al cuadrado, es igual al primero.

La raíz cuadrada de x se expresa:

Las raíces cuadradas fueron uno de los primeros desarrollos de las matemáticas, siendo particularmente investigadas durante el periodo pitagórico, cuando el descubrimiento de que laraíz cuadrada de 2 era irracional (inconmensurable) o no expresable como cociente alguno, lo que supuso un hito en la matemática de la época.

Posteriormente se fue ampliando la definición de raíz cuadrada. Para los números reales negativos, la generalización de la función raíz cuadrada de éstos da lugar al concepto de losnúmeros imaginarios y al cuerpo de los números complejos, algo necesario para que cualquier polinomio tenga todas sus raíces (teorema fundamental del álgebra). La diagonalizaciónde matrices también permite el cálculo rápido de la raíz de una matriz.

Ecuación de primer grado simple

Una ecuación es una igualdad que sólo se verifica para unos valores concretos de una variable, generalmente llamada x.

Resolver una ecuación consiste en hallar los valores de la variable que hacen cierta la igualdad.

Recuerda:

Si un elemento está sumando en un miembro pasa al otro restando. Si está restando pasa sumado.

Si un número multiplica a todos los elementos de un miembro pasa al otro dividiendo y si los divise pasa multiplicando.

A continuación les dejo un vídeo de como resolver ecuaciones de primer grado

GUIA PARA EXAMEN FLOR 1C

EL MAESTRO NOSDIO UNA GUIA O UNAS INSTRUCCIONES PARA ESTUDIAR Y ESTOS SON: ·PERIMETRO ·SUPERFISIE ·AREA ·SOLUCION DE PROBLEMAS DE PROPORCIONALIDAD(TIPO RESETA) ·EL AREA DEL CIRCULO ·DIVICION CON PUNTO DECIMAL ·SOLUCION DE ECUASIONES ·ECUACIONES ·CALCULO DE PERIMETRO PERO LOS TENIAMOS QUE ESTUDIAR Y ULTIMAMENTE Y ALGO DIFISILES JAJA BUENO ME DESPIDO .

LAS BALANZAS FLOR 1 - C

VIDEO BALANZA ASER LA VALANZA FUE LA INSPIRACION PARA RESOLVER LAS ECUASIONES O TAMBIEN LA PODEMOS DIBUJAR PERO TAMBIEN PUEDE SER DIBERTIDO YA QUE JUEGAS CON EL Y ADEMAS CONVIVES CONTUS COMPAÑEROS.

TECNICA.

LUNES 22 DE MARZO DEL 2011.

EL VIERNES 18 DE MARZO ISIMOS TECNICA BUENO COMO SIEMPRE LA ASEMOS TODOS LOS VIERNES

LA TECNICA TRATO DEECU LAS ASIONES:

1-50x+70=5593 YLA (X) SIGNIFICA=110.46

2-10X+34=74 YLA (X) SIGNIFICA=4

3-5X+15=3X+15 YLA (X) SIGNIFICA= 6 Y 10. EL RESULTADO = 45

4-12X+15018X+3 YLA (X) SIGNIFICA=2 Y 2. EL RESULTADO = 39

Y NOS DIO SU CORREO DE GMAIL QUE ES = elprofrmigeulengel@gmail.com

PASOS PARA UNA RAIZ CUADRADA.

Separa los dígitos de dos en dos. .
La mejor manera de explicar cómo se hace una raíz cuadrada es con un ejemplo. Vamos a hacer la raíz cuadrada del número 64.253. El número a partir de ahora se llamará radicando, el símbolo de la raíz será radical y cada cajetilla que abramos para hacer operaciones renglón de la raíz. El primer paso consiste en separar los dígitos del radicando de dos en dos de derecha a izquierda. Si hubiera decimales hay que dividir primero los enteros de derecha a izquierda y después la parte decimal a la inversa, de izquierda a derecha. En este caso no pueden quedar dígitos individuales, por lo que añadiremos un cero cuando lo necesitemos.

Busca un número que multiplicado por sí mismo se acerque a tu primer dígito. .
Hay que buscar un número cuyo cuadrado (multiplicar por si mismo) se acerque, nunca pase, la primera cifra del radicando, que en nuestro caso es 6. El número que encontremos lo apuntamos en el segundo renglón de la raíz, llamados auxiliares porque nos ayudan a descifrarla. La primera incógnita es 2, que al multiplicarse por si mismo da 4. Ese número hay que restarlo ahora al radicando (6-4) y anotar debajo el resultado (2).

Baja los otros dos dígitos y sigue la operación. .
Sigue estos pasos: Baja las dos siguientes cifras del radicando (42), sube la primera incógnita a la primera casilla (2) y escribe su doble en la tercera auxiliar. Una vez realizado esto seguimos con la operación. Vuelve a separar los dígitos del radicando que nos queda (242) dejando fuera la última cifra (2). Ahora divide el primer grupo de dígitos entre el número que haya en la tercera auxiliar (24/4). La cifra resultante la debes poner junto al dígito del tercer auxiliar y multiplicar por esa misma cifra (46X6) y comprobar que el resultado no es superior al radicando que tenemos. Si lo supera, debes bajar un número la incógnita.

Baja más dígitos y sube la segunda incógnita arriba. .
En nuestro ejemplo 46X6 son 276, lo que supera a 242, por lo que debemos utilizar el 5, y la operación es 45X5=225. Resta el resultado al radicando: 225-242=17. Ahora baja los siguientes dos dígitos (53) y después sube el 5 junto al 2.

En el cuarto renglón auxiliar escribe el doble de lo que tenga el primero. .
Llegados a este paso tenemos el radicando 1753 y en el cuarto auxiliar hay que poner el doble de los dos dígitos ya resueltos (25), que sería 50.

Separa el radicando y divide por la última incógnita. .
Volvemos a descartar el último número del radicando y nos queda 175. Lo volvemos a dividir por lo que ponga en el cuarto auxiliar, 175/50 y el resultado es 3 (hay que descartar los decimales). Volvemos a escribir la incógnita y multiplicar por ella misma: 503X3=1509.

Vuelve a restar. .
Restamos el resultado al radicando y nos queda 244.

Si no hay más dígitos se acaba la raíz cuadrada. .
La incógnita la volvemos a subir al renglón raíz y como ya no nos quedan más dígitos en el radicando, la raíz cuadrada se acaba. Si en el radicando hubiera decimales, deberiamos poner una coma junto al 253 y seguir resolviendo como los pasos anteriores.

Busca una calculadora... .
Si tienes cerca una calculadora te puedes ahorrar el resto de pasos. Si la calculadora que vas a utilizar es la del ordenador te enseñamos a hacerlo, porque no aparece el icono de raíz cuadrada. Lo primero es abrir la calculadora (Iniciio/Todos los programas/Accesorios/Calculadora). Después, despliega la pestaña 'Ver' y selecciona 'Científica'. A continuación, escribe el radicando, 64253, selecciona la palabra Inv. que está a la izquierda y pincha la tecla en rosa que encontrarás abajo donde indica x al cuadrado.
.

tecnica de 1 - c

VIERNES 25 DE FEBRERO DEL 2011.

E n el salón hicimos la técnica que el maestro MIGUEL ANGEL (de matemáticas) nos puso 6 preguntas y estas son las siguientes:

1_. Pepe a obtenido las siguientes calificaciones en los siguientes 5 periodos de matemáticas y desea saber cuál es su promedio:
8.7, 8.8, 9.1, 10 y 9.2.

R= 7.36

2_. Hugo, Paco y Luis reunieron 286 canicas y las van a repartir explica cual sería la mejor forma de hacerlo.

R= Mejor empiezo pro la división que se divide 285 entre 3 y nos da resultado de 95.33.Nos da a resultado si multiplicamos 95.33x3 nos da a resultado de 285, entonces nos sobra una canica pero a quien se las damos. Por eso lo mejor sería darle la canica a quien junto más canicas o echarla a un frasco y volver a comenzar
a juntar canicas.

3_. Para hacer un papalote chino se debe cubrir la superficie de un aro de bambú, si el radio es de este círculo es de 21.5 y consideramos Pi como 3.14. ¿Cuál SERIA EL AREA?

R= primero se multiplica 21.5 x 21.5=462.25 y luego multiplicas 462.25 x 3.14 = 1451.465 ese sería el resultado sería R=1451.465

4_. Para cubrir esa superficie circular de un papalote de 1451.465 cm 2
Hacerlo con 5 colores diferentes si se hace un reparto equitativo , ¿Qué cantidad de superficie cubrirá cada color?

R= Aquí primero se debe de dividir 1451.465 entre 5 para que nos dé la respuesta de 290.293 cm 2.

5_. En casa de Rafa se reunieron Lalo, Rosa y Arturo para hacer una tarea de español , como ya eran las 20hrs y aun no acababan se organizaron para pedir una pizza y refresco que dando en repartirse en partes iguales, ¿Cuánto debe aportar cada uno si el total fue de 212.55pesos?

R= Pues primero se divide para ver cuanto va a aportar cada quien para pagar lo mismo o la misma cantidad de dinero. Y entonces la división nos da el resultado de 53.175 como resultado Y ya lo multiplicas por 3 para que compruebes el resultado.

CUBOS MAGICOS

LUNES 21 DE FEBRERO DEL 2011.

HOY LUNES EN LO QUE EL MAESTRO LLEGABA NUESTRA MONITORA
ROSA (DE MATEMATICAS),NOS PUSO UNTRABAJO DE COMPLETAR UN
CUBO MAGICO.QUE DESIA ASI:

Completa el siguiente cuadro magico sumando sus lados
dando un resultado de = 15.siendo en todos los lados
con el resultado de quince(vertical ,horisontal y
diagonales).
Ese cubo seles mostrara al lado derecho.
15 15 15 15 15
15 4 9 2 15
15 3 5 7 15
15 8 1 6 15
15 15 15 15 15

graficas "1-c"

JUVES 10 DE FEBRERO DEL 2011.

HOY EL MAESTRO NOSDIO EL PROMEDIO DE LOS 3PERIODOS Y DIJO QUE MI FILA SACARA
EL PROMADIO DE EL 2PERIODO Y SALIMOS MUY BAJOS POR QUE EL RESULTADO FUE DE 7.7
PERO AQUI LO MALO ES QUE DE LAS CALIFICASIONES LA MAS AL TA FUE 6, DE HAY LE
SIGUE 8,DESPUES SIGUE 7 Y POR ULTIMO LAS CALIFICASIONES DE 10 Y DE 9 QUEDARON
EMPATES Y SON MUY POCAS PERSONAS LAS QUE SACARON 9 Y 10.

papalotes 1

MIERCOLES 9 DE FEBRERO DEL 2011.

HOY NOSOTROS NOSTOCO TRAER NUESTRO PAPALOTE Y EL MAESTRO SI NOLO REBISO PERO NOS DIJO QUE SALIERAMOS A LAS CANCHAS DE LA ESCUELA Y QUE SACARAMOS EL PAPALOTE PARA
BOLARLO PERO EL MIO NI QUISO BOLAR NADAMAS SE ALSO UN POCO, PERO SE QUISO QUEDAR EN EL PISO Y NO BOLAR.

papalotes

JUEVES 3 DE FEBRERO DEL 2011.

HOY TENEMOSQUE ASER UN PAPALOTE CON LA FORMA QUE NOSOTROS QUERAMOS HASTA LO
PODEMOS DISEÑARLO EN NUESTRO CUADERNO DE MATEMETICAS Y LLEBARLO A LA ESCUELA
PARA DE MOSTRAR QUE LO PODEMOS LLEBAR A LA ESCUELA TALBES EL LUNES 7 DE FEBRERO
DEL 2011.

Técnica

1° La señora rosa horneo 5.6 kg de galletas y debe hacer bolsitas de 250 gr ¿Cuántas bolsas llenara completamente?

4

250/1000 4 250

0 * 5 * 2

____ ______

20 500

llenara completamente 22 bolsas

2° El reloj de pared de mi mamá tiene un diámetro de 32cm si lo quiero rodear con un listón ¿Cuánto necesito? Considera pi=3.14

3.14 Necesitare 100.48 cm. de listón

* 32

________

628

942

_________

100.48

3° Si yo fui al Internet y me lleve $20 y la hora cuesta $10 y las impresiones $1.5 cada una , si tuve que sacar 3 impresiones y ocupe 1/2 hora el Internet ¿Cuánto fue y cuanto cambio me dieron?

5

2/10 1.50 4.50

0 * 3 + 5.00

______ _______

4.50 9.50

20.00

- 9.50

Gastara $9.50 y le sobrara $10.50

_____

10.50

Estas fueron algunas preguntas de la técnica y pues estas venian en el examen el cual el maestro nos dara la calificación mañana

matematicas de primero "c".

Miércoles 2 de febrero del 2011.
Hoy entregamos unos cubos de papiroflexia e isimos un examen que venía con varios problemas como el siguiente ejemplo:
1- La señora María horneo 5.6kg de galletas y debe hacer bolsitas de 325g ¿Cuántas bolsitas llenara completamente?
R= 22 Bolsitas.